2018. 10. 30. 04:01 알고리즘&자료구조/푼 문제
Baekjoon 3146
'알고리즘&자료구조 > 푼 문제' 카테고리의 다른 글
| Baekjoon 10565 (0) | 2018.10.01 |
|---|---|
| Backjoon 10227 (0) | 2018.09.20 |
| Baekjoon 7644 (0) | 2018.09.19 |
2018. 10. 30. 04:01 알고리즘&자료구조/푼 문제
| Baekjoon 10565 (0) | 2018.10.01 |
|---|---|
| Backjoon 10227 (0) | 2018.09.20 |
| Baekjoon 7644 (0) | 2018.09.19 |
2018. 10. 30. 03:57 알고리즘&자료구조/이론
| Hasse diagram (0) | 2018.09.30 |
|---|---|
| Min-max heap (0) | 2018.09.29 |
| 부분합 (0) | 2018.09.24 |
| 그래프의 표현 (0) | 2018.09.24 |
| 트리의 지름 (0) | 2018.09.24 |
2018. 10. 1. 02:38 알고리즘&자료구조/푼 문제
자, 여기 N개의 회사가 있다. 각각의 회사에는 최고위 인사, 즉 모두에게 직간접적으로 상사인 사람이 하나 있고, 나머지 직원들은 모두 각각 자신의 상사를 가지고있다. Y가 X의 직접적인 상사이거나, 또는 X의 상사가 Y의 부하직원 일 경우 모두 X는 Y의 부하직원이라고 하기로 한다.
어느 날 인사팀에서는 회사에 급여 불균형이 얼마나 심한지 조사해보기로 했다. 주어진 인사정보에서, 사원 A에 대한 급여 불균형은 A및 A의 모든 부하직원의 급여 중 최대값과 최소값의 차를 말한다.
인사팀은 모든 사원들에 대한 급여 불균형을 빠르게 계산할 수 있기를 원한다. 그러나, 조사 도중 어느 사원 및, 해당 사원의 모든 부하직원의 급여가 오르는 경우가 있기 때문에, 이는 굉장히 복잡한 작업이다. 좀 도와주실 수 있는지?
입력으로는
- 회사 수 (최대 20)
그리고 각 회사에 대해
- 사원 수 (2 <= N <= 1,000,000)
- 각 사원의 상사 번호 (모든 사원은 1부터 N까지의 유일한 번호가 매겨진다. 해당 라인의 입력은 N-1개의 숫자가 주어지며 K번째 번호는 K+1번의 번호를 가진 사원의 상사를 뜻한다.)
- 각 사원의 급여 (N개의 숫자, K번째 번호는 K번 사원의 급여를 뜻한다.)
- 처리할 명령의 수 (1 <= Q <= 10,000)
그리고 각 명령에 대해
- 처리할 명령의 이름 및 그에 따르는 숫자
- 'Q'의 경우, 같은 라인에 주어지는 다음 숫자의 사원에 대한 급여 불균형 조사 (ex, Q 2)
- 'R'의 경우, 같은 라인에 주어지는 다음 숫자의 사원 및 해당 사원의 모든 부하직원의 급여를 사원 번호 다음의 숫자만큼 인상 (ex, R 4 2)
K번호를 가진 사원의 상사의 번호는 K보다 작다. 초기 급여는 1부터 1000까지이다. 급여 인상은 1000을 넘지 않는다.
출력으로는
각각의 급여 불균형 조사에 대해 한 라인에 하나씩 결과를 출력.
내 가정:
다시 트리 문제인듯 하다.
인접 리스트로 각각의 사원에 대해 직속 부하직원에 대한 단방향 그래프를 만들어주었다 (Q 명령에 대해 아래로 탐색해 나가기 위해서)
또 각 사원의 급여 정보는 배열로 관리하였다.
매 Q 명령마다 트리를 탐색하여, Min-max heap에 넣어 최대값 및 최소값을 도출하였다.
R의 명령 역시 트리를 탐색하며 급여 정보를 수정해주었다.
결과는 역시 시간초과.
매 명령마다 트리를 탐색하는게 문제인거같은데, DP로 접근하는 방법이 있으려나?
10/01/2018
이 상황에서 Min-max heap이 의미가 있는지? Min-max heap을 떼어내고, 순회했던 트리에 대해 최소값과 최대값을 기억하도록 해보았다.
X에 대한 Q 명령이 주어졌을 때, 리프 노드에서 X 노드까지 최소값 및 최대값을 전달, 기억하여, X의 서브트리에 대해 Q 명령이 다시 주어질 경우 다시 순회를 하지 않아도 되도록 해보았다.
R 명령이 주어졌을 때에는 X 서브트리를 순회하며 해당 사원들의 salary를 모두 올려주고, 만약 노드가 기억하고 있는 최소값 및 최대값이 있을 경우 해당 값 또한 salary 인상값만큼 올려주었다(해당 노드의 서브트리가 갖는 모든 노드에 해당하는 사원의 salary가 올랐으므로)
그리고 다시 X로 돌아와, 부모 노드가 기억하는 최소값과 최대값이 존재할 경우(X 서브트리를 포함하여 최소값 및 최대값 조사가 이루어진 적이 있음을 뜻함) 계속 부모 노드로 거슬러 올라가며 최소값과 최대값을 새로 갱신해주도록 하였다.
그래서 결과는? 시간초과
10/30/2018
세그먼트 트리를 이용하는 문제였다.
Q 명령이 주어졌을 때, 살펴야 하는 범위를 구하기 위해 각 사원의 번호들을 재정의해 줄 필요가 있다.
트리를 구성한 후, 오일러 트리 순회를 통해 방문하는 노드 순서로 각 사원의 번호를 재정의해주고, 해당 사원이 갖는 부하직원들의 번호 범위 또한 정의해 줄 수 있다.
또한 R 명령의 경우에 Lazy approach를 적용하면 제한시간 내에 문제를 해결할 수 있다.
| Baekjoon 3146 (0) | 2018.10.30 |
|---|---|
| Backjoon 10227 (0) | 2018.09.20 |
| Baekjoon 7644 (0) | 2018.09.19 |
2018. 9. 30. 19:11 알고리즘&자료구조/이론
하세 다이어그램은 유한부분순서집합을 표현하기 위한 도표, 도형이다. 집합의 각 요소들은 정점으로 표현되며, 정점간의 관계는 각 정점의 상대적 높이, 그리고 정점을 잇는 선분으로 표현된다. x, y를 잇는 선분의 경우, 자기 자신 이외의 다른 선분을 교차하는 것이 가능하나, 해당 선분이 나타내는 관계에 포함된 두 정점 이외의 정점을 가로질러서는 안된다.
y 정점이 x 정점보다 높은 곳에 위치하고, 두 정점은 선분으로 이어져 있을 경우. x < y이며 x < z < y 인 정점 z가 존재하지 않음을 나타낸다.
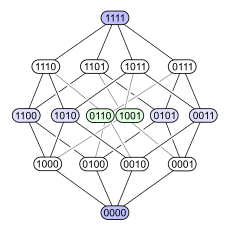
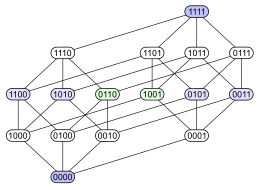

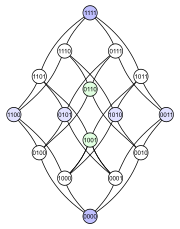
하나의 유한부분순서집합에서 나올 수 있는 다양한 하세 다이어그램(출처 : 영문 위키피디아)
위에서 볼 수 있듯 표현하고 싶은 관계가 직관적으로 나타나는 하세 다이어그램을 그리는것이 중요하다.
또한 그래프 그림과는 독립적으로, 하세 다이어그램은 일방향 비순환 그래프를 뜻하기도 한다?
| Segment tree, Lazy approch (0) | 2018.10.30 |
|---|---|
| Min-max heap (0) | 2018.09.29 |
| 부분합 (0) | 2018.09.24 |
| 그래프의 표현 (0) | 2018.09.24 |
| 트리의 지름 (0) | 2018.09.24 |
2018. 9. 29. 04:06 알고리즘&자료구조/이론
Min-max heap은 min heap과 max heap의 장점을 취해 구현한 완전이진트리이다.
홀수번째 깊이의 노드들은 min heap을, 짝수번째 깊이의 노드들은 max heap을 구성한다.
기존 min heap, max heap과 같이
을 가지면서도 min, max값에 대해 모두 상수 참조시간을 갖는 매력적인 자료구조이다.
구현에는
함수가 필요하다.
heapify 연산의 경우 첫번째 인덱스를 1로 갖는 배열로 구현한 트리의 경우
기존 힙과 같이 인덱스 size(tree) / 2 부터 1까지(자식을 갖는 노드들을 아래에서 위로 거슬러 올라감, n번째 깊이의 노드들은 n-1번째 깊이의 노드들보다 먼저 연산되어야 한다) 거꾸로 TrickleDown 연산을 수행해주면 된다.
TrickleDown 연산을 보자
procedure TrickleDown(i)
i는 array내의 위치를 뜻함
if i는 min level then
TrickleDownMin(i)
else
TrickleDownMax(i)
endif
procedure TrickleDownMin(i)
if A[i]가 children을 가지고있음 then
m := A[i]의 children 및 grandchildren 중
(존재하는 경우에) 가장 작은 요소의 인덱스
if A[m]이 A[i]의 grandchild임 then
if A[m] < A[i] then
swap(A[m], A[i])
if (A[m] > A[m의 부모]) then
swap(A[m], A[m의 부모])
endif
TrickleDownMin(m)
endif
else A[m]이 A[i]의 child임
if A[m] < A[i] then
swap(A[i], A[m])
endif
endif
TrickleDownMax의 경우 TrickleDownMin에서 부등호의 방향만 다르게 구현해주면 된다.
해당 자료구조가 갖는 성질에 비해 구현이 매우 쉽고 간단하다.
기본적으로 A[i]의 grandchild, child를 살펴 가장 작은값(A[m])을 살펴 swap할지를 결정하는데,
A[i]가 그 어느값보다 작을 경우:
이미 해당 min level의 성질을 만족함, 더이상 연산을 수행할 필요 없음.
A[m]이 child일 경우:
A[i]와 A[m]의 위치만 swap 후 종료, 삭제의 경우 이미 트리는 min-max heap의 성질을 만족하는 상태이며,
heapify중일 경우에는 heapify 연산이 아래 레벨부터 위의 레벨 순서로 TrickleDown을 수행하기 때문에 swap된 기존 A[m]값은 자연히 올라갈것임.
A[m]이 grandchild일 경우:
A[i]와 A[m]의 위치를 바꾸고, 또 A[m]의 부모와 비교하여 값이 A[m]이 더 클경우 A[m]과 A[m의 부모]를 swap한다.
이는 기존의 A[i]값이 max heap level에 속해야 할 값이었을 경우 leaf노드 끝까지 내려갔다가 다시 올라오는 연산을 할 수고를 덜게해준다.
기존 A[i]값이 더 상위의 max heap level에 속해야 할 값이라면, heapify 연산중에는 상기한 바와 같이 자연히 올라가게 될 것이다.
삭제의 경우에는 이미 트리는 min-max heap의 성질을 만족하는 상태이기에, 이전 i의 grandparent의 TrickleDownMin 연산에서 max heap level에 속했어야 옳다
마지막으로 grandchild와 swap에 성공했을 경우엔 TrickleDownMin을 또 다시 호출하여 min-max heap의 성질을 만족할 때까지 내려가도록 한다.
procedure Deletion(i)
A[i] := A[length]
length := length - 1
TrickleDown(i)
procedure Insertion(K)
A[length] := K
BubbleUp(length)
length := length + 1
마지막으로 insertion에 쓰이는 BubbleUp의 경우 TrickleDown보다도 더 간단하다.
procedure BubbleUp(i)
i는 array내의 위치를 뜻함
if i는 min level then
if i의 부모 존재 then
if A[i] > A[i의 부모] then
swap(A[i], A[i의 부모])
BubbleUpMax(i의 부모)
else
BubbleUpMin(i)
endif
endif
else
if i의 부모 존재 then
if A[i] < A[i의 부모] then
swap(A[i], A[i의 부모])
BubbleUpMin(i의 부모)
else
BubbleUpMax(i)
endif
endif
endif
procedure BubbleMinUp(i)
if A[i]가 grandparent를 가짐 then
if A[i] < A[i의 grandparent] then
swap(A[i], A[i의 grandparent])
BubbleUpMin(i의 grandparent)
endif
endif
역시 BubbleMaxUp의 경우 부등호의 방향만 다르게 해주면 된다.
먼저 A[i]자신의 min, max level 여부를 살피고 반대되는 성질의 level(A[i]의 parent가 위치한 level)에 진입할 수 있는지를 확인한다
A[i]가 min level이고 A[i]의 parent보다 클 경우 : max heap level로 진입
A[i]가 min level이고 그 외 : min heap level로 진입
A[i]가 max level이고 A[i]의 parent보다 작을 경우 : min heap level로 진입
A[i]가 max level이고 그 외 : max heap level로 진입
그리고 BubbleMinUp, BubbleMaxUp 각각에서는 min-max heap의 성질을 만족할 때까지 계속 grandparent와 비교하며 요소를 위로 swap해주면 된다.
이렇게 구현된 min-max heap의 경우 root노드는 min값을, 그리고 root의 자식노드 둘 중 하나가 max값을 가지게 된다.
| Segment tree, Lazy approch (0) | 2018.10.30 |
|---|---|
| Hasse diagram (0) | 2018.09.30 |
| 부분합 (0) | 2018.09.24 |
| 그래프의 표현 (0) | 2018.09.24 |
| 트리의 지름 (0) | 2018.09.24 |
2018. 9. 24. 22:42 알고리즘&자료구조/이론
| Segment tree, Lazy approch (0) | 2018.10.30 |
|---|---|
| Hasse diagram (0) | 2018.09.30 |
| Min-max heap (0) | 2018.09.29 |
| 그래프의 표현 (0) | 2018.09.24 |
| 트리의 지름 (0) | 2018.09.24 |
2018. 9. 24. 22:41 알고리즘&자료구조/이론
그래프를 표현하는 방법 중에는 매트릭스를 이용한 인접 매트릭스와 리스트를 이용한 인접 리스트가 있다.
<인접 매트릭스>
<인접 리스트>
| Segment tree, Lazy approch (0) | 2018.10.30 |
|---|---|
| Hasse diagram (0) | 2018.09.30 |
| Min-max heap (0) | 2018.09.29 |
| 부분합 (0) | 2018.09.24 |
| 트리의 지름 (0) | 2018.09.24 |
2018. 9. 24. 22:40 알고리즘&자료구조/이론
트리에서 두 정점을 잇는 경로 중 가장 큰 가중치(긴 거리)를 갖는 경로를 트리의 지름이라고 한다.
이는 트리에서 임의의 정점을 택하고, 해당 정점에서 가장 멀리 떨어진 정점 w를 찾고, 다시 정점 w에서 가장 멀리 떨어진 정점 d를 찾으면 쉽게 구할 수 있다.
p는 점 또는 선이다.
x에서 가장 멀리 떨어진 정점 w가
1. w일 경우: d, w는 트리 내에서 가장 멀리 떨어진 점이므로 다음으로 찾을 정점은 d가 될것이다.
2. d일 경우: 상동.
3. d, w가 아닌 다른 정점 y일 경우: a, b사이의 거리를 d(a, b)라 할때, d(y, p) > d(d, p), d(w, p)가 되므로 y가 트리의 지름에 속해야 옳다.
| Segment tree, Lazy approch (0) | 2018.10.30 |
|---|---|
| Hasse diagram (0) | 2018.09.30 |
| Min-max heap (0) | 2018.09.29 |
| 부분합 (0) | 2018.09.24 |
| 그래프의 표현 (0) | 2018.09.24 |
2018. 9. 20. 00:16 알고리즘&자료구조/푼 문제
세로, 가로 각각 R, C의 크기을 갖는 매트릭스 안에서 세로, 가로 각각 H, W의 크기로 (1 ≤ H ≤ R, 1 ≤ W ≤ C) 구성가능한 모든 서브매트릭스들의 중앙값들 중 가장 작은 값을 찾아야 한다.
매트릭스의 각 요소 k의 값은 1 ≤ k ≤ R * C이고 유일하다. H, W는 모두 홀수이고 R, C는 각각 1에서 3000 사이의 수이다.
내 가정:
왼쪽 위 서브매트릭스부터 오른쪽 아래 서브매트릭스까지 전수 조사, 중앙값은 파이썬 list의 sort 함수를 이용해보았다. 역시 실패.
sort가 문제일까?, 중앙값 찾는것을 이진탐색퀵셀렉션으로 바꾸어보았다. 실패.
전수조사가 문제겠군... 한번 서브매트릭스 내에 지금까지 구한 최소값보다 작은 값이 있을경우에만 중앙값을 구하도록 해보자. 실패.
이제 어떻게 바꾸지 도무지 종을 잡을 수 없던 도중, 고맙게도 해당 문제에 대해 질문을 해주신 분을 통해 특정 값을 미리 지목 후 해당 값이 답이 될 수 있는지 조사하는 방법도 있다는걸 깨달았다. 내일 해봐야겠다. 이 글이 푼 문제로 이동하길 바라며.
9/22/2018
틀린 단어 수정: 이진탐색->퀵셀렉션, 이진탐색은 정렬된 배열에서 특정한 수를 찾는것(O(log(n))). 퀵셀렉션은 정렬되지 않은 리스트에서 k번째 크기의 수를 찾는것(좋은 pivot의 경우 O(n), 나쁜 pivot의 경우 O(n^2)).
문제 링크 수정
09/24/2018
풀이:
부분합을 이용하여 어느 값 x (1 ≤ x ≤ R * C)에 대해 x가 중앙값이 될 수 있는지, 또 x보다 작은, 중앙값이 될 수 있는 값이 있는지 탐색가능하다.
O(RC + (R-H)(C-W)) 시간 소요.
위 매트릭스는 해당 문제에 대한 예제 입력중 하나이다. 3x3 서브매트릭스에 대해 x=13값이 중앙값이 될 수 있는지 살펴보자.
먼저 요소에 k에 대해 k = x일 경우 0을, k < x일 경우 -1을, k > x일 경우 1을 매핑해주자.
결과로 다음과 같은 매트릭스가 나온다. 이제 우리는 서브매트릭스의 SUM값에 따라 해당 서브매트릭스에서 값 x가 중앙값인지(SUM=0), x보다 작은값이 중앙값이 될 수 있는지(SUM < 0)를 알아낼 수 있다.
그러나 모든 서브매트릭스에 대해 일일이 SUM을 수행할 경우 O(RCHW)라는 무지막지한 시간이 소요된다.
이를 부분합을 통해 O(RC + (R-H)(C-W))로 줄일 수 있다.
부분합 매트릭스의 경우 다음과 같이 나온다. 이 때 밝은 부분이 나타내는 서브매트릭스의 SUM값을 D-C-B+A를 수행해 구할 수 있다.
이를 통해 값 x에 대한 모든 서브매트릭스의 SUM값 탐색을 (R-H)(C-W)번으로 수행할 수 있다.
이 때
1. 0보다 작은 SUM값이 있을 경우: 더 작은 x값에 대한 중앙값 가능 여부 탐색.
2. 0보다 작은 SUM값이 없고, 0이 되는 SUM값이 있을 경우: 해당 값이 답.
3. 그 외(SUM값이 모두 0보다 크다): 더 큰 x값에 대한 중앙값 가능 여부 탐색.
을 수행하면 된다.
x값 탐색에 대해서는 이진 탐색을 이용할 경우 해당 문제에 대한 시간 복잡도는 총 O((RC + (R-H)(C-W))log(RC)) -> O(RClog(RC))가 되겠다.
| Baekjoon 3146 (0) | 2018.10.30 |
|---|---|
| Baekjoon 10565 (0) | 2018.10.01 |
| Baekjoon 7644 (0) | 2018.09.19 |
2018. 9. 19. 00:37 알고리즘&자료구조/푼 문제
상부에 조르고 졸라 드디어 내 도시에도 고속도로가 들어서게 되었다. 만세!
문제는, 그냥 다들 한곳에 모여살면 좋을것을 서로 원수라도 졌는지 공동체들이 여기저기 흩어져 있다는 것.
공동체들은 각각 유일한 번호로 이름지어져 있고, 각 공동체들을 잇는 도로가 존재한다.
한 공동체에서 다른 공동체로 갈 수 있는 경로는 꼭 하나만(가) 존재한다.
우리는 이 도로중 일부를 대체할 하나의 선으로 이루어진 고속도로를 짓는다. 고속도로에서 떨어져있는 공동체는 어쩔 수 없이 기존에 존재하던 도로를 이용해 고속도로에 접근해야한다.
고속도로에서 가장 멀리 떨어진 공동체에서 고속도로까지의 거리를 최소화하는 방향으로 고속도로를 건설하였을 때, 그 거리는 얼마인가?
내 가정:
각 노드에서 다른 노드까지의 경로가 단 하나만(가) 존재한다는 것으로 보아 이 그래프는 트리이다.
고속도로는 그래프의 한 종단노드에서 다른 종단노드까지의 경로를 잇는 선이다.
각 종단노드들을 루프토드로 잡고 아래로 탈탈 털어 트리모양으로 만든 후, 각 루프노드에서 각 리프노드까지 경로의 코스트를 구한 경우의 수들 중, 코스트가 가장 큰 경로1를 우리가 지을 고속도로로 한다.
이제 고속도로가 지나는 노드 중, 고속도로에 접하지 않은 노드를 갖는 노드들을 루프노드들로 하고, 고속도로가 이어지지 않은 리프노드들까지의 코스트들을 구해 가장 큰 값을 취한다.
09/24/2018
풀이:
트리의 지름을 구하는 문제이다.
트리의 지름의 각 끝점이 되는 두 종단노드를 구한 후, 해당 두 종단노드를 잇는 경로에서 두 종단노드를 제외한 다른 종단노드까지의 거리중 가장 큰 값을 구하면 된다.
트리의 지름의 각 끝점이 되는 두 종단노드 x, y를 구한 후, x, y를 잇는 경로의 cost를 0으로 설정, x부터 시작해 트리를 DFS하여 가장 큰 코스트를 출력하였다.
| Baekjoon 3146 (0) | 2018.10.30 |
|---|---|
| Baekjoon 10565 (0) | 2018.10.01 |
| Backjoon 10227 (0) | 2018.09.20 |